Hoofdstuk 27 Factoriële ANOVA
- factoriële designs
- lineaire model
- interactie
- moderatie.
- Onderzoekspracticum experimenteel onderzoek (PB0422)
27.1 Inleiding
Het hoofdstuk Variantieanalyse bespreekt de one-way ANOVA, een analysemethode voor onderzoeksdesigns met één numerieke afhankelijke variabele (bijvoorbeeld depressieve symptomen) en één nominale predictor variabele (bijvoorbeeld interventie 1/interventie 2/wachtlijst). De nominale predictor bestaat per definitie uit verschillende categorieën, die bij een experiment meestal condities worden genoemd. Wanneer er slechts twee condities zijn, dan is de one-way ANOVA gelijk aan een onafhankelijke \(t\)-test.
Maar wat nou als je verwacht dat het effect van de experimentele condities afhangt van een andere variabele? Je wilt bijvoorbeeld onderzoeken of de interventies (interventie 1, interventie 2, wachtlijst) een aanvullend effect hebben in combinatie met medicatie (medicatie, placebo). Op het moment dat je combinaties van nominale predictoren maakt, spreken we over een factorieel onderzoeksdesign.
In dit hoofdstuk staat de factoriële ANOVA centraal, de analysemethode die geschikt is om factoriële designs te analyseren. Er zijn vele varianten van de factoriële ANOVA, maar meestal wordt met deze term de onafhankelijke factoriële ANOVA (independent factorial ANOVA) bedoeld. De onafhankelijke factoriële ANOVA is een uitbreiding van de one-way ANOVA naar een ANOVA met twee of meer onafhankelijke variabelen op nominaal meetniveau, ook wel factoren genoemd. In de context van experimenten wordt het design behorend bij deze analyse soms ook wel een volledig gerandomiseerd factorieel design genoemd (completely randomized factorial design).
Een factorieel design onderscheidt zich van andere ANOVA’s omdat de niveaus van een factor worden geëvalueerd in combinatie met andere factoren. Eenvoudiger gezegd: in een factorieel design worden combinaties gemaakt van alle mogelijke condities van de onafhankelijke variabelen. Bijvoorbeeld, wanneer er in een onderzoek naar behandelsucces twee variabelen worden gemanipuleerd – type behandeling (controle/experimenteel) en medicijn (placebo/medicijn) – dan is er sprake van een factorieel design als er vier condities zijn: controle-placebo, controle-medicijn, experimenteel-placebo en experimenteel-medicijn.
In een factorieel design wordt iedere proefpersoon dus toegewezen aan een niveau van twee of meer onafhankelijke variabelen. Als er twee condities zijn in de eerste factor (in dit voorbeeld de behandeling) en twee in de tweede factor (hier: medicijn), dan noemen we dit een 2x2-factorieel design. Zo kan er ook een 3x2-design zijn, als er drie en twee condities zijn enzovoort.
Traditioneel wordt deze techniek, net als de one-way ANOVA, behandeld als een uitbreiding van een verschiltoets, zoals de \(z\)- of \(t\)-toets. Deze variantieanalysebenadering, waarbij de nadruk ligt op het opsplitsen van alle kwadratensommen, vrijheidsgraden en de \(F\)-test, spreekt in beginsel goed tot de verbeelding, maar het wordt lastiger om de meer geavanceerde punten te begrijpen. In dit boek kiezen we er daarom voor om dit type modellen te bespreken en analyseren aan de hand van het lineaire model, zoals dat bij regressieanalyse wordt gebruikt. Uiteraard maakt dat voor de uiteindelijke resultaten en conclusies niet uit.
In het lineaire model behorend bij factoriële ANOVA wordt de afhankelijke variabele voorspeld door twee of meer nominale (of ordinale) variabelen, in de experimentele context vaak factoren genoemd. Naast deze factoren worden ook altijd de interacties tussen deze factoren in het model betrokken. Eigenlijk is dat het grootste verschil met de one-way ANOVA. In dit hoofdstuk bespreken we het lineaire model behorend bij factoriële ANOVA en leggen daarbij de nadruk op de betekenis van de interactie en het daaraan gerelateerde begrip moderatie.
Net als bij de one-way ANOVA, is er een \(F\)-waarde met bijbehorende vrijheidsgraden die getoetst kan worden op statistische significantie. In deze \(F\)-toets zijn alle factoren en hun interacties betrokken. De \(F\)-waarde is ook hier een verhouding tussen modelvariantie (signaal) en residuele variantie (ruis). Ook kunnen dezelfde effectmaten worden gebruikt als bij one-way ANOVA. Verder kunnen er net als bij de one-way ANOVA ook bij factoriële designs post-hoc-testen of contrasten worden gebruikt om specifieke hypotheses te toetsen.
27.2 Assumpties factoriële ANOVA
De assumpties van een factoriële ANOVA zijn niet anders dan die van andere ANOVA’s. Zie de bespreking van de assumpties in het hoofdstuk Variantieanalyse.
Kort samengevat:
De residuele meetfout is normaal verdeeld met een gemiddelde van nul.
De variantie is homoscedastish: de variantie van de afhankelijke variabele is gelijk tussen de groepen.
De scores op de afhankelijke variabele zijn onafhankelijk van elkaar.
Er is geen verstoring door uitbijters.
27.3 Interactie en moderatie
27.3.1 Interactie
In factoriële designs zijn er meerdere onafhankelijke variabelen die ieder een effect kunnen hebben op de afhankelijke variabele. Het effect van een onafhankelijke variabele op een afhankelijke variabele wordt een hoofdeffect genoemd. Als de effecten van de onafhankelijke variabelen in het model samen opgeteld kunnen worden om de afhankelijke variabele te verklaren, dan is er sprake van een additief effect: het geheel is de som van de delen.
In modellen met meerdere onafhankelijke variabelen kan het ook zijn dat het effect van een onafhankelijke variabele niet op zichzelf staat, maar afhangt van de waarde van een andere onafhankelijke variabele. Het effect van een variabele \(A\) op \(Y\) kan bijvoorbeeld afzwakken naarmate de waarde van de onafhankelijke variabele \(B\) toeneemt.
Wanneer het effect van een variabele op een afhankelijke variabele afhangt van de waarde van een andere variabele, dan spreken we van een interactie-effect. Een interactie-effect is anders dan een additief effect, omdat het totale effect nu meer óf minder is dan de som van de delen. Om de afhankelijke variabele te voorspellen, kunnen de effecten niet simpelweg opgeteld worden, maar moet er ook rekening gehouden worden met een multiplicatief effect.
Stel dat onderzoekers willen weten of prestatie een optelling is van talent en inzet. In een studie onderzoeken ze of intelligentie en het aantal uren studeren voorspellers zijn voor hogere tentamencijfers. Het effect van intelligentie op tentamencijfers is een hoofdeffect, net als het effect van het aantal uren studeren op tentamencijfers.
Maar, de onderzoekers ontdekken dat de tentamencijfers niet goed te voorspellen zijn uit een simpele optelling van de effecten van intelligentie en het aantal uren studie. Ze vinden namelijk dat een toename van het aantal uren studie alleen sterk voorspellend is voor hogere tentamencijfers voor hoogintelligente deelnemers. Voor midden- en laagintelligente deelnemers blijkt een toename van het aantal uren studie slechts een matige tot geen voorspellende waarde te hebben voor hun tentamencijfers.
Gemiddeld genomen is er misschien wel een positief (hoofd)effect van aantal uren studie op tentamencijfers, maar het zou de data tekort doen om met zo’n botte bijl over de meerwaarde van studie-uren te spreken. De relatieve meerwaarde van meer uren studeren moet bekeken worden in de context van iemands intelligentie: mensen die hoogintelligent zijn, halen veel meer uit ieder uur studie dan deelnemers die minder intelligent zijn.
Het kan dus zijn dat er gemiddeld genomen een hoofdeffect is van een onafhankelijke variabele op een afhankelijke variabele, maar dit hoofdeffect kan niet meer op zichzelf bekeken worden zodra het effect van de variabele afhangt van een andere variabele. Om dit meer inzichtelijk te maken, geven we hier een getallenvoorbeeld van wat interactie-effecten inhouden en hoe ze verschillen van additieve effecten, dus wanneer er geen interactie is.
Als voorbeeld nemen we een 2x2-factoriële ANOVA met twee between-subjectfactoren \(A\) en \(B\), ieder met twee niveaus \(0\) en \(1\).
| B = 0 | B = 1 | |
|---|---|---|
| A = 0 | 6 | 7 |
| A = 1 | 4 | 5 |
In dit voorbeeld is er geen sprake van interactie, maar van twee additieve effecten. Het verschil tussen \(A=0\) en \(A=1\) is onafhankelijk van de waarde van \(B\). Het verschil is altijd \(2\) (\(6-4=2\); \(7-5=2\)). Hetzelfde geldt voor het effect van \(B\). Dit is onafhankelijk van de waarde van \(A\), namelijk een verschil van \(1\) (\(6-7 = 4-5\)).
Een interactie is meer (of minder) dan de som van de delen. Neem bijvoorbeeld de volgende situatie (Tabel 27.2):
| B = 0 | B = 1 | |
|---|---|---|
| A = 0 | 1 | 4 |
| A = 1 | 7 | 6 |
Het effect van \(A\) en \(B\) is niet additief. In conditie \(B=0\) is het gemiddelde verschil tussen \(A=0\) en \(A=1\) gelijk aan \(6\) (\(7-1=6\)) en in conditie \(B=1\) is het gemiddelde verschil tussen \(A=0\) en \(A=1\) gelijk aan \(2\) (\(6-4=2\)). Het effect van \(A\) hangt dus af van de waarde van \(B\).
Omgekeerd hangt het effect van \(B\) op de afhankelijke variabele ook af van de waarde van \(A\) (\(1-4 ≠ 7-6\)). Er is hier dus sprake van een interactie-effect. Statistisch gezien maakt het geen verschil of het effect van \(A\) op \(Y\) afhangt van \(B\) of omgekeerd. Wanneer er hypotheses worden geformuleerd, wordt er één van beide interpretaties gekozen. Dit zal nader besproken worden bij het begrip moderatie.
Er zijn vele soorten interactie-effecten. Meestal wordt er een onderscheid gemaakt tussen kwantitatieve en kwalitatieve interacties. De volgende tabel (Tabel 27.3): zet cijfermatig de twee soorten interacties naast elkaar.
| B = 0 | B = 1 | B = 0 | B = 1 | |
|---|---|---|---|---|
| A = 0 | 2 | 1 | 2 | 6 |
| A = 1 | 5 | 3 | 5 | 3 |
Een kwantitatieve interactie is een interactie waarbij de sterkte van het effect op de afhankelijke variabele van bijvoorbeeld \(B\), afhangt van de waarde van \(A\), maar waarbij de richting van het effect van \(B\) hetzelfde is ongeacht de waarde van \(A\). Dit wordt vaak een versterkend of verzwakkend effect genoemd. Iets neemt bijvoorbeeld toe over de tijd, maar sterker in de ene dan in de andere groep.
In de tabel is bijvoorbeeld te zien dat, wanneer \(A=0\), de waarde van de afhankelijke variabele \(1\) minder is als \(B=1\) dan als \(B=0\) (\(2-1=1\)), maar dit verschil is \(2\) als \(A=1\) (\(5-3=2\)). Dus het verschil tussen \(B=0\) en \(B=1\) hangt af van de waarde van \(A\), maar in beide gevallen leidt \(B=1\) tot een lagere gemiddelde score dan \(B=0\).
Bij een kwalitatieve interactie hangen zowel de sterkte als de richting van het effect van \(B\) op de afhankelijke variabele af van de waarde van \(A\). Afhankelijk van hoe het interactiepatroon eruitziet, wordt dit soms een kruislingse interactie genoemd. In de tabel is bijvoorbeeld te zien dat \(A=1\) gemiddeld tot een toename leidt in de afhankelijke variabele als \(B=0\), maar juist tot een afname als \(B=1\).
Onderstaande Figuur 27.1 illustreert de interacties uit de tabel. De figuur verduidelijkt wat het verschil is tussen een kwantitatieve interactie, waarbij slechts de sterkte van een effect varieert, maar de richting hetzelfde blijft, en een kwalitatieve interactie, waarbij zowel de sterkte als de richting van een effect verschillen.
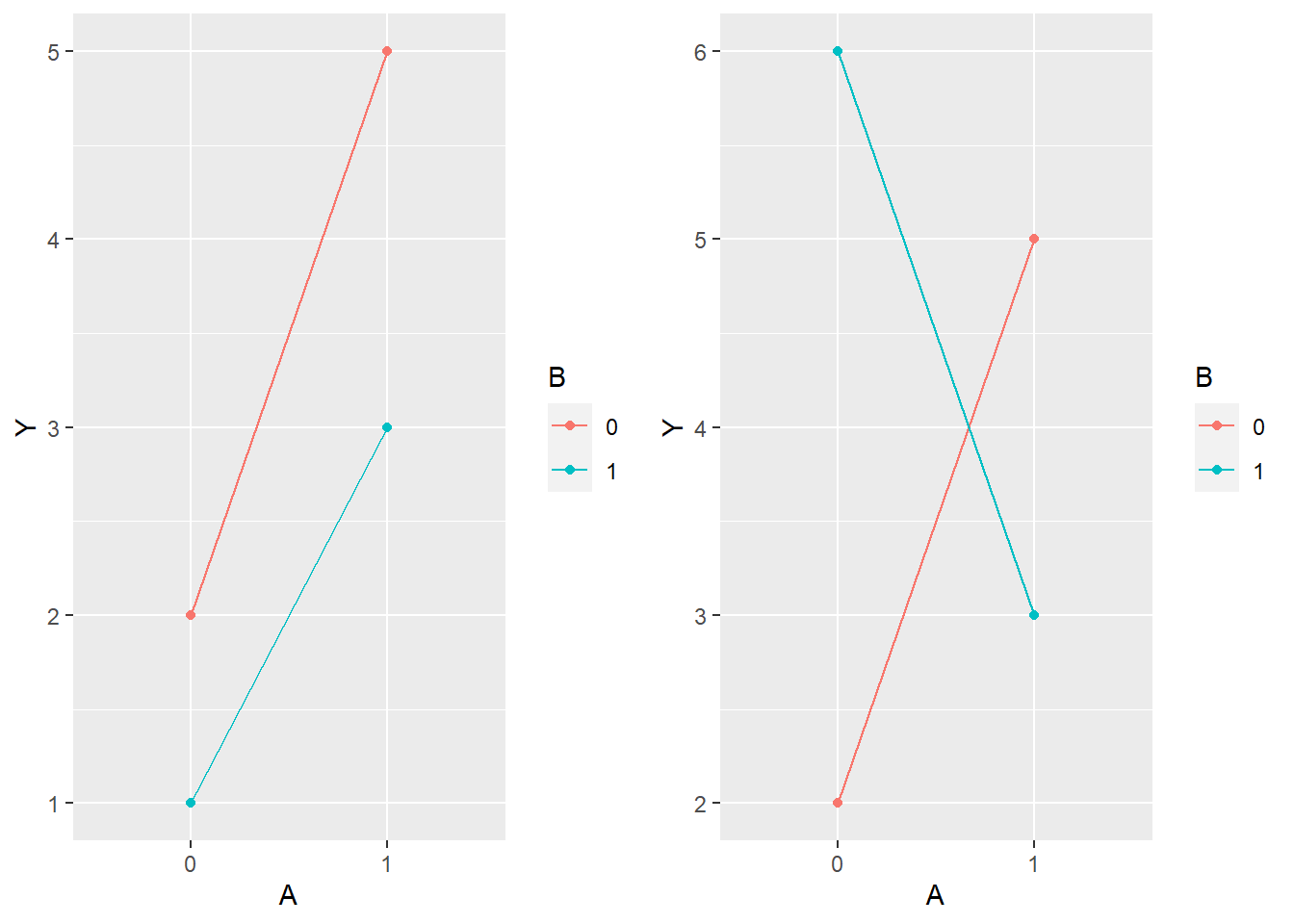
Figuur 27.1: Voorbeeld van een kwantitatief en kwalitatief interactie-effect
Vooral bij kwalitatieve interacties kan het zo zijn dat er géén statistische hoofdeffecten worden gevonden. In de figuur is bijvoorbeeld te zien dat door het kruislingse karakter van de interactie er gemiddeld genomen geen effect is van \(A\). Wanneer je de waarde van \(B\) namelijk buiten beschouwing laat, is de gemiddelde waarde van de afhankelijke variabele bij \(A=0\) \(4\) (\((2+6)/2\)) en bij \(A=1\) ook \(4\) (\((5+3)/2\)). Er kan dus sprake zijn van een interactie-effect zonder dat er (significante) hoofdeffecten zijn. Het is daarom altijd belangrijk om in de statistische analyse zowel de hoofd- als de interactie-effecten te evalueren.
Bij het interpreteren van de uitkomst maakt het een groot verschil of er een interactie-effect is. Wanneer er sprake is van een interactie-effect, is het onmogelijk om de hoofdeffecten los van de interactie te beschrijven. Het effect van één variabele is namelijk conditioneel op een andere variabele. We spreken dan van conditionele hoofdeffecten. Met andere woorden, bij het beschrijven van het effect van een variabele op \(Y\) moet altijd de andere variabele betrokken worden. Statistisch worden hoofd- en interactie-effecten los van elkaar geëvalueerd. Maar zodra er sprake is van interactie, zal het interpreteren van het model altijd op het niveau van de interactie zijn en worden de losse hoofdeffecten niet besproken.
27.3.2 Moderatie
Een moderator is een variabele die het verband tussen twee andere variabelen beïnvloedt. Dit betekent dat het effect van de predictor op de afhankelijke variabele anders is voor mensen die hoog scoren op de moderator dan voor mensen die laag scoren op de moderator. Een moderator kan een groepsindeling representeren, zoals een experimentele factor.
Een voorbeeld ter verduidelijking. Stel dat men door voorlichting te geven veilig verkeersgedrag, zoals minder hard rijden, wil bevorderen. Er zijn twee condities van de experimentele factor ‘voorlichting’: voorlichting die communiceert over de hoogte van de boete voor onveilig gedrag (1) en voorlichting over het aantal slachtoffers van onveilig gedrag (2). Daarnaast wordt een tweede factor gemanipuleerd, namelijk de wijze van voorlichting, ook met twee condities: via een folder (1) of via een gesproken tekst door acteurs (2).
De uitkomsten van het onderzoek laten zien dat de voorlichting over slachtoffers beter werkt, maar alleen in combinatie met de gesproken tekst. Bij voorlichting via een folder is er geen verschil tussen beide condities. De wijze van voorlichting is hier de moderator die het effect van het soort voorlichting (de predictor) beïnvloedt.
De moderator is hier een categorische of dichotome (twee categorieën) variabele, maar een moderator kan in principe ook een intervalvariabele zijn, zoals een eigenschap die iemand in meer of mindere mate bezit (bijvoorbeeld veerkracht). Bij een intervalvariabele zijn er geen natuurlijke groepen, maar we kunnen nog steeds mensen onderscheiden die relatief hoog scoren op zo’n variabele en mensen die relatief laag op scoren.
Theoretisch gezien kan een moderatie-effect verschillende vormen aannemen. Een moderator kan een effect of een verband laten verschijnen of versterken. De tegenhanger daarvan is dat een moderator een verband kan laten verdwijnen of afzwakken. In een derde situatie is het verband positief dan wel negatief, afhankelijk van de waarde van de moderator.
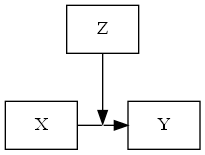
Figuur 27.2: Moderatiemodel
In Figuur 27.2 staat het moderatiemodel in algemene vorm weergegeven. De variabele \(X\) is de predictor, zoals een experimentele factor, en \(Y\) is de afhankelijke variabele. De variabele \(Z\) is de moderator in dit model. In experimentele designs is dit ook een experimentele factor. Omdat moderatiemodellen een causaal proces veronderstellen, moet hier in het onderzoeksdesign rekening mee worden gehouden. Ideaal bezien worden zowel de predictor als de moderator experimenteel gemanipuleerd en worden deelnemers random toebedeeld aan de verschillende condities.
Een moderatiemodel is een theoretisch model waarin causale verwachtingen worden beschreven, waarbij er een onderscheid wordt gemaakt tussen predictor en moderator. Om een moderatiemodel te onderzoeken wordt een statistisch model getoetst, waarin de interactie tussen de moderator en predictor is opgenomen. In zo’n statistisch model is er echter geen onderscheid tussen moderator en predictor. Beide hebben de rol van voorspellende variabele.
Welke variabele de rol van moderator krijgt en welke de rol van predictor is puur theoretisch. Het statistisch model kan daar niets over zeggen. Wanneer uit de analyse van het statistisch model blijkt dat de interactie significant is, kun je op basis van het theoretisch model concluderen dat er sprake is van moderatie en op basis van de effectgroottes uitrekenen hoe die moderatie er precies uitziet.
Kort samengevat kun je stellen dat moderatie gelijk is aan interactie, waarbij de variabelen respectievelijk het label van moderator en predictor krijgen op basis van theoretische overwegingen.
27.4 Het lineair model van factoriële ANOVA
27.4.1 Voorbeeld: data over slaapkwaliteit
De meest simpele factoriële ANOVA met slechts één factor is in feite gelijk aan de one-way ANOVA. In het hoofdstuk over one-way ANOVA werden data over slaapkwaliteit gebruikt als voorbeeld. De afhankelijke variabele was de gerapporteerde slaapkwaliteit en er was één predictor (factor) – ‘avondactiviteit’ – die bestond uit drie condities: lezen, sporten en controle (geen instructie).
Naast de factor ‘avondactiviteit’ introduceren we nu een tweede factor: ‘drank’. Deze factor bestaat uit twee categorieën (condities): koffie en water. De deelnemers van het onderzoek werden willekeurig toebedeeld aan een van deze condities, waarbij ze of de hele avond een hoeveelheid koffie moesten drinken, of enkel water.
De twee factoren waren volledig gebalanceerd, wat wil zeggen dat alle combinaties van condities mogelijk waren en dat in elke combinatie van condities ongeveer evenveel deelnemers zaten. Er waren dus \(3x2\) combinaties waarin een deelnemer kon vallen: lezen-koffie, lezen-water, sporten-koffie, sporten-water, controle-koffie en controle-water.
In Figuur 27.3 zie je de data waarbij de gemiddelden van de zes condities worden aangegeven met een horizontale lijn. Vooral de twee ‘sporten’-condities verschillen van elkaar: de sportende deelnemers die water moesten drinken, scoren hoger op slaapkwaliteit dan de sportende deelnemers die koffie hebben gedronken. Voor de groep lezers en de controlegroep maakt het niet heel veel uit of ze water of koffie dronken.
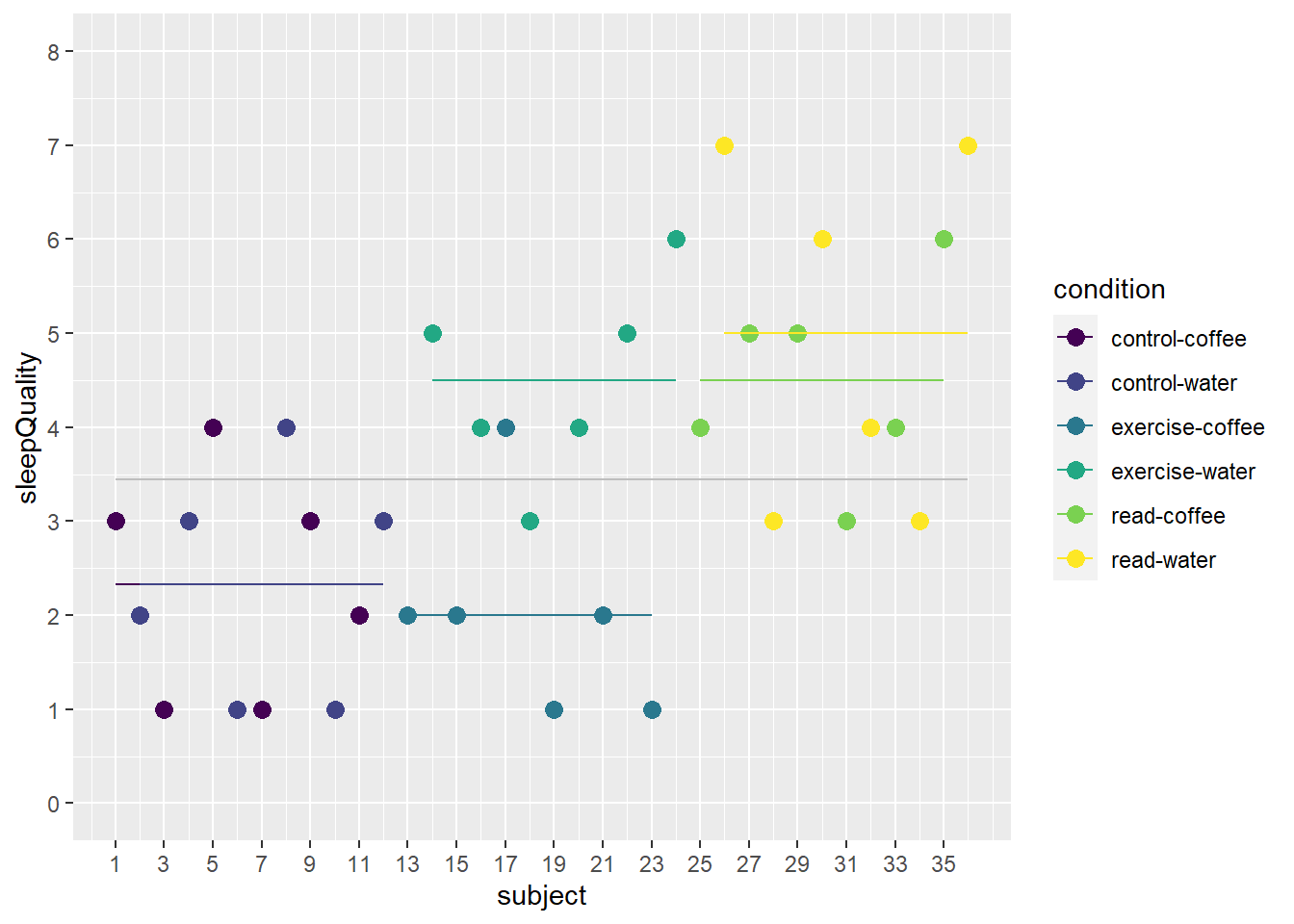
Figuur 27.3: Voorbeelddata over slaapkwaliteit in factorieel design
Dit is een voorbeeld van een interactie-effect. Het drinken van koffie ten opzichte van water werkt anders voor de verschillende condities van ‘avondactiviteit’. Koffiedrinken heeft vooral een negatief effect op de slaapkwaliteit bij de avondactiviteit sporten, maar weinig effect bij de avondactiviteit lezen of geen instructie.
27.4.2 Lineair model
Het uitvoeren van een factoriële ANOVA kan ook aan de hand van het lineaire regressiemodel. Voor het huidige voorbeeld kan dit lineaire model als volgt worden uitgeschreven:
\[\begin{equation} sleepQuality = b_0 + b_1exercise + b_2read + b_3coffee + \epsilon \tag{27.1} \end{equation}\]
De variabele ‘exercise’ is, net als bij de one-way ANOVA, een dummyvariabele die de waarde \(1\) heeft bij een persoon die in de conditie ‘sporten’ zit en anders \(0\) is. De variabele ‘read’ is ook een dummyvariabele, die de waarde \(1\) heeft bij een persoon die in de conditie ‘lezen’ zit en anders \(0\) is. Nieuw is de dummyvariabele ‘coffee’, die \(1\) is bij personen die koffiedrinken en anders \(0\). Omdat deze variabele maar twee categorieën heeft, verwijst de \(0\) hier naar de mensen die water hebben gedronken. De categorie ‘water’ is voor de variabele ‘coffee’ de zogenaamde referentiecategorie.
Uit het model blijkt dat iemands’ slaapkwaliteit kan worden voorspeld door de groep waarin die zich bevindt. Als iemand bijvoorbeeld in de controleconditie van de factor ‘avondactiviteit’ valt en in de conditie ‘water’ van de factor ‘drank’, dan zijn ‘exercise’, ‘read’ en ‘coffee’ allemaal gelijk aan \(0\). Voor deze mensen wordt de voorspelde slaapkwaliteit weergegeven door alleen het intercept (weergegeven met \(b_0\) in de formule van het regressiemodel).
We analyseren nu deze data met het lineaire regressiemodel. Zie Tabel 27.4 voor de schattingen van de parameters \(b_0\), \(b_1\), \(b_2\) en \(b_3\). Hier geeft \(b_0\) het intercept aan, \(b_1\) de coëfficiënt behorend bij de dummyvariabele ‘exercise’, oftewel behorend bij de conditie ‘sporten’, en \(b_2\) de coëfficiënt behorend bij de dummyvariabele ‘read’, oftewel de conditie ‘lezen’. Nieuw is \(b_3\), de coëfficiënt behorend bij de dummyvariabele ‘coffee’, oftewel de conditie ‘koffie’. Naast de puntschattingen van deze dummyvariabelen, bevat de tabel ook de \(95\)%-betrouwbaarheidsintervallen.
| Estimate | Std. Error | t value | Pr(>|t|) | 2.5 % | 97.5 % | |
|---|---|---|---|---|---|---|
| (Intercept) | 2.83 | 0.46 | 6.2 | 0.000 | 1.90 | 3.76 |
| exerciseD | 0.92 | 0.56 | 1.6 | 0.111 | -0.22 | 2.06 |
| readD | 2.42 | 0.56 | 4.3 | 0.000 | 1.28 | 3.56 |
| coffeeD | -1.00 | 0.46 | -2.2 | 0.036 | -1.93 | -0.07 |
In Tabel 27.5 staan de effectgroottes van het gehele model en voor elke parameter: de partiële omega-kwadraten. Het effect van lezen op de slaapkwaliteit blijkt het grootst.
| Omega2_partial | CI_low | CI_high | |
|---|---|---|---|
| model | 0.37 | 0.12 | 1 |
| 2 | 0.10 | 0.00 | 1 |
| 3 | 0.52 | 0.19 | 1 |
| 4 | 0.19 | 0.00 | 1 |
De \(F\)-waarde bij deze analyse met bijbehorende vrijheidsgraden is: \(F\)( 3,32) = 7.93, \(p < .001\), \(\omega^2\) = 0.37 met \(90\)%-betrouwbaarheidsinterval [0.12, 1]. Welch’s \(F\) (waarbij wordt aangenomen dat de varianties ongelijk zijn) is: \(F\)( 5,13.95) = 6.13, \(p\) = 0.
De door het model voorspelde waarden voor elke conditie kunnen met behulp van de formule van het lineaire model en de parameterschattingen worden afgeleid.
Allereest berekenen we de voorspelde waarde van slaapkwaliteit voor de mensen in de controlegroep van ‘avondactiviteit’ die ‘water’ hebben gedronken. Voor deze groep zijn de waarden van de dummyvariabelen ‘exercise’, ‘read’ en ‘coffee’ gelijk aan \(0\). Als we deze waarden invullen in de formule dan wordt de voorspelling:
\[\begin{equation} \begin{split} sleepQuality(controle, water) = b_0 + b_1 \times (0) + b_2 \times (0) + b_3 \times (0) = \\ 2.83 + 0.92\times 0 + 2.42\times 0 + -1\times 0 = 2.83 \end{split} \tag{27.2} \end{equation}\]
De voorspelde waarde van slaapkwaliteit in deze groep is dus 2.83.
Op deze manier kunnen we voor alle zes de condities een voorspelde waarde berekenen. Als tweede en laatste voorbeeld nemen we de mensen die in de ‘lezen’ conditie van ‘avondactiviteit’ zitten en in de ‘koffie’ conditie van ‘drank’. In het lineaire model vullen we nu voor de dummyvariabelen ‘read’ en ‘coffee’ een \(1\) in. De dummyvariabele ‘exercise’ blijft \(0\).
\[\begin{equation} \begin{split} sleepQuality(read, coffee) = b_0 + b_1 \times (0) + b_2 \times (1) + b_3 \times (1) = \\ 2.83 + 0.92\times 0 + 2.42\times 1 + -1\times 1 = 4.25 \end{split} \tag{27.3} \end{equation}\]
Omdat de \(F\)-toets een significant resultaat oplevert, kunnen we concluderen dat de gemiddelden van de zes groepen (condities) van elkaar verschillen. De parameterschattingen suggereren dat fysieke inspanning in de avond tot een betere slaapkwaliteit leidt en dat het lezen van een boek de slaapkwaliteit nog meer verbetert. Verder lijkt het drinken van koffie een negatief effect te hebben op de slaapkwaliteit.
27.5 Model met interactietermen
In tegenstelling tot bij one-way ANOVA, zien we de voorspellingen van de condities niet exact terug in Figuur 27.3. De reden hiervoor is dat het onderliggende model niet compleet is. Er zijn namelijk alleen hoofdeffecten meegenomen voor de factoren ‘avondactiviteit’ en ‘drinks’ en niet de interactie-effecten tussen deze variabelen.
Zoals we eerder zagen, betekent een interactie-effect dat het effect van een variabele afhangt van de waarde van een andere variabele. Als er geen interactie-effect is tussen twee predictorvariabelen op een afhankelijke variabele, dan is het gezamenlijke effect van deze twee simpelweg de som van de twee afzonderlijke effecten.
Dit was in feite een aanname bij het eerdergenoemde lineaire model: er werd verondersteld dat de effecten op de slaapkwaliteit van bijvoorbeeld ‘sporten’ en ‘koffie’ onafhankelijk van elkaar zijn. In werkelijkheid kunnen effecten elkaar ook versterken of verzwakken. Misschien is het effect van koffiedrinken wel veel sterker als je de hele avond leest, dan wanneer je sport.
Om dit te onderzoeken voegen we een interactieterm toe aan het model voor elk paar van variabelen. Omdat het om een interactie tussen twee predictorvariabelen gaat, noemen we dit een tweeweg-interactie. Een interactieterm wordt (meestal) gevormd door de twee variabelen met elkaar te vermenigvuldigen; het product is dan de interactieterm.
Bij twee numerieke variabelen is er één interactieterm, maar bij twee nominale variabelen kun je elke categorie minus de referentiecategorie van een variabele combineren met alle categorieën minus de referentiecategorie van de andere variabele. Anders gezegd, we kunnen de dummyvariabelen behorend bij de verschillende nominale variabelen met elkaar vermenigvuldigen om interactietermen te maken.
In het voorbeeld over slaapkwaliteit kunnen we de categorieën van de variabele ‘avondactiviteit’, namelijk ‘exercise’ en ‘read’ (controle is de referentie), combineren met de categorie ‘coffee’ van de variabele ‘drinks’ (de categorie ‘water’ is de referentiecategorie). Er zijn dus twee interactietermen mogelijk: exercise*coffee en read*coffee. Het * symbool geeft aan dat het om een interactieterm gaat. Het lineair regressiemodel met de interactietermen kan als volgt worden uitgeschreven:
\[\begin{equation} sleepQuality = b_0 + b_1exercise + b_2read + b_3coffee + b_4(exercise * coffee) \\ + b_5(read * coffee) + \epsilon \tag{27.4} \end{equation}\]
| Estimate | Std. Error | t value | Pr(>|t|) | 2.5 % | 97.5 % | |
|---|---|---|---|---|---|---|
| (Intercept) | 2.3 | 0.53 | 4.44 | 0.000 | 1.26 | 3.41 |
| exerciseD | 2.2 | 0.74 | 2.92 | 0.007 | 0.65 | 3.68 |
| readD | 2.7 | 0.74 | 3.59 | 0.001 | 1.15 | 4.18 |
| coffeeD | 0.0 | 0.74 | 0.00 | 1.000 | -1.52 | 1.52 |
| exerciseD:coffeeD | -2.5 | 1.05 | -2.38 | 0.024 | -4.65 | -0.35 |
| readD:coffeeD | -0.5 | 1.05 | -0.48 | 0.638 | -2.65 | 1.65 |
De resultaten van deze analyse staan in Tabel 27.6. De \(F\)-waarde bij deze analyse met bijbehorende vrijheidsgraden is: \(F\)( 5,30) = 6.67, \(p\) < .001, \(\omega^2\) = 0.44 met \(90\)%-betrouwbaarheidsinterval [0.14, 1].
De parameterschattingen van deze analyse corresponderen nu weer met de gemiddelden uit Figuur 27.3. De meest linkse, gekleurde horizontale lijn is bijvoorbeeld het intercept, \(b_0 =\) 2.33. Dit getal is precies het gemiddelde van de slaapkwaliteitsscores van de mensen die in de controleconditie van ‘avondactiviteit’ vielen en water dronken.
Op dezelfde manier als bij het model zonder interacties kunnen we voor alle zes de condities een voorspelde waarde berekenen, bijvoorbeeld de door dit model voorspelde waarde van slaapkwaliteit van de mensen in de conditie ‘lezen en koffie’. In het lineaire model vullen we nu net als eerder voor de dummyvariabelen ‘read’ en ‘coffee’ een \(1\) in en de dummyvariabele ‘exercise’ blijft \(0\). De interactietermen zijn het product van twee dummyvariabelen. Een interactieterm krijgt alleen de waarde \(1\) als beide dummyvariabelen de waarde \(1\) hebben. In dit geval heeft de dummyvariabele read*coffee dus de waarde \(1\) en exercise*coffee de waarde \(0\).
\[\begin{equation} \begin{split} & sleepQuality(read, coffee) = \\ & b_0 + b_1\times (0) + b_2\times (1) + b_3\times (1) + b_4\times (0) + b_5\times (1) = \\ & 2.33 + 2.17\times 0 + 2.67\times 1 + 0\times 1 + -2.5\times 0 + -0.5\times 1 = 4.5 \end{split} \tag{27.5} \end{equation}\]
Deze waarde komt exact overeen met het gemiddelde van deze groep in Figuur 27.3. We zouden voor iedere groep een voorspelde waarde van slaapkwaliteit kunnen uitrekenen en dan zou blijken dat deze allemaal precies gelijk zijn aan de groepsgemiddelden zoals getoond in de figuur. De reden dat dit model perfecte voorspellingen geeft, is dat het model alle mogelijke termen bevat.
De analyse maakt duidelijk dat er in het effect op de slaapkwaliteit een interactie is tussen het soort avondactiviteit en wat men drinkt. Specifiek komt naar voren dat de combinatie koffiedrinken en sporten de slaapkwaliteit verslechtert. We kunnen nu niet zomaar spreken van het hoofdeffect van ‘avondactiviteit’. We moeten deze variabele altijd interpreteren in relatie tot de variabele ‘drinks’. Zo is de waarde die achter ‘exercise’ staat niet het effect van ‘exercise’ in het algemeen, maar het effect van ‘exercise’ voor personen die water hebben gedronken.
27.6 Simple effects
Wanneer we het effect van één bepaalde variabele (factor) bekijken, voor een bepaalde waarde van een andere variabele (factor), spreken we van simple effects of enkelvoudige effecten. Deze simple effects kunnen inzicht geven in hoe het interactie-effect uitpakt. Wanneer er geen interactie-effect is, zijn alle simple effects van een variabele ongeveer gelijk aan het hoofdeffect van die variabele.
Laten we als voorbeeld de simple effects van de variabele ‘avondactiviteit’ bekijken voor de waarde ‘coffee’ van de variabele ‘drank’. Omdat ‘avondactiviteit’ een nominale variabele is, bestaat deze uit twee dummyvariabelen. We kunnen dit als volgt schrijven:
\[\begin{equation} \begin{split} & sleepQuality('avondactiviteit'|coffee) = \\ & b_0 + b_1\times exercise + b_2\times read + b_3\times (1) + \\ & b_4\times exercise + b_5\times read = \\ & (b_0+b_3) + (b_1+b_4)\times exercise + (b_2+b_5)\times read = \\ & 2.33 + -0.33 \times exercise + 2.17 \times read \end{split} \tag{27.6} \end{equation}\]
Voor iemand uit de conditie ‘read’ (die koffie heeft gedronken) is de voorspelde slaapkwaliteit:
\[\begin{equation} \begin{split} & 2.33 + -0.33 \times (0) + 2.17 \times (1) = \\ & 2.33 + 2.17 = 4.5 \end{split} \tag{27.7} \end{equation}\]
De dummy variabele ‘read’ krijgt hier dus de waarde \(1\) en ‘exercise’ de waarde \(0\). Voor iemand uit de conditie ‘exercise’ (die koffie heeft gedronken) is de voorspelde slaapkwaliteit:
\[\begin{equation} \begin{split} & 2.33 + -0.33 \times (1) + 2.17 \times (0) = \\ & 2.33 + -0.33 = 2 \end{split} \tag{27.8} \end{equation}\]
De simple effects van ‘avondactiviteit’ voor de waarde ‘water’ van de variabele ‘drank’ kunnen op dezelfde manier worden uitgerekend:
\[\begin{equation} \begin{split} & sleepQuality('avondactiviteit'|water) = \\ & b_0 + b_1\times exercise + b_2\times read + b_3\times (0) + b_4\times (0) + b_5\times (0) = \\ & b_0 + b_1\times exercise + b_2\times read = \\ & 2.33 + 2.17 \times exercise + 2.67 \times read \end{split} \tag{27.9} \end{equation}\]
Vul \(1\) in voor ‘exercise’ en \(0\) voor ‘read’ om de simple effects van ‘exercise’ te krijgen of vul \(1\) in voor ‘read’ en \(0\) voor ‘exercise’ om de simple effects van ‘read’ te krijgen, in beide gevallen voor mensen die water hebben gedronken.
27.7 Moderatiehypothese
In het voorgaande voorbeeld is getoond dat er een interactie-effect bestaat tussen het type avondactiviteit en wat men drinkt in het voorspellen van de slaapkwaliteit. Dit voorbeeld is uitgewerkt aan de hand van het bijbehorende statistische model. Maar hoe zit het in dit voorbeeld met moderatie? Hiervoor hebben we een theoretisch model nodig.
Een theoretisch model zou kunnen stellen dat de variabele avondactiviteit een voorspeller is van slaapkwaliteit. De avondactiviteit is dan de predictorvariabele en slaapkwaliteit de afhankelijke variabele. Een bijpassende hypothese zou kunnen zijn dat het effect van de avondactiviteit op de slaapkwaliteit afhangt van wat men drinkt. Meer specifiek zou de hypothese kunnen luiden: het drinken van koffie in de avond verzwakt het positieve effect van lichamelijke inspanning op de slaapkwaliteit. In dit theoretische model is de drankinname (koffie versus water) de moderator. Bepaalde dranken (hier: koffie) versterken (of verzwakken) het effect van de lichamelijke inspanning.
In een ander theoretisch model zouden de rollen van drank en lichamelijk inspanning omgedraaid kunnen zijn. Een bijpassende hypothese zou dan zijn: het drinken van koffie in vergelijking met water verslechtert de slaapkwaliteit, en dit effect is sterker als er ’s avonds wordt gesport. Beide theoretische modellen kunnen dus leiden naar hetzelfde statistische model. De analyse van de interactie bepaalt of er sprake is van interactie of moderatie, maar de theorie bepaalt hoe die moderatie geïnterpreteerd wordt.
27.7.1 De moderatie gevisualiseerd
Het moderatie-effect (of interactie-effect) kan worden gevisualiseerd door de simple effects uit te rekenen en die te plotten in een figuur. Zie Figuur 27.4.
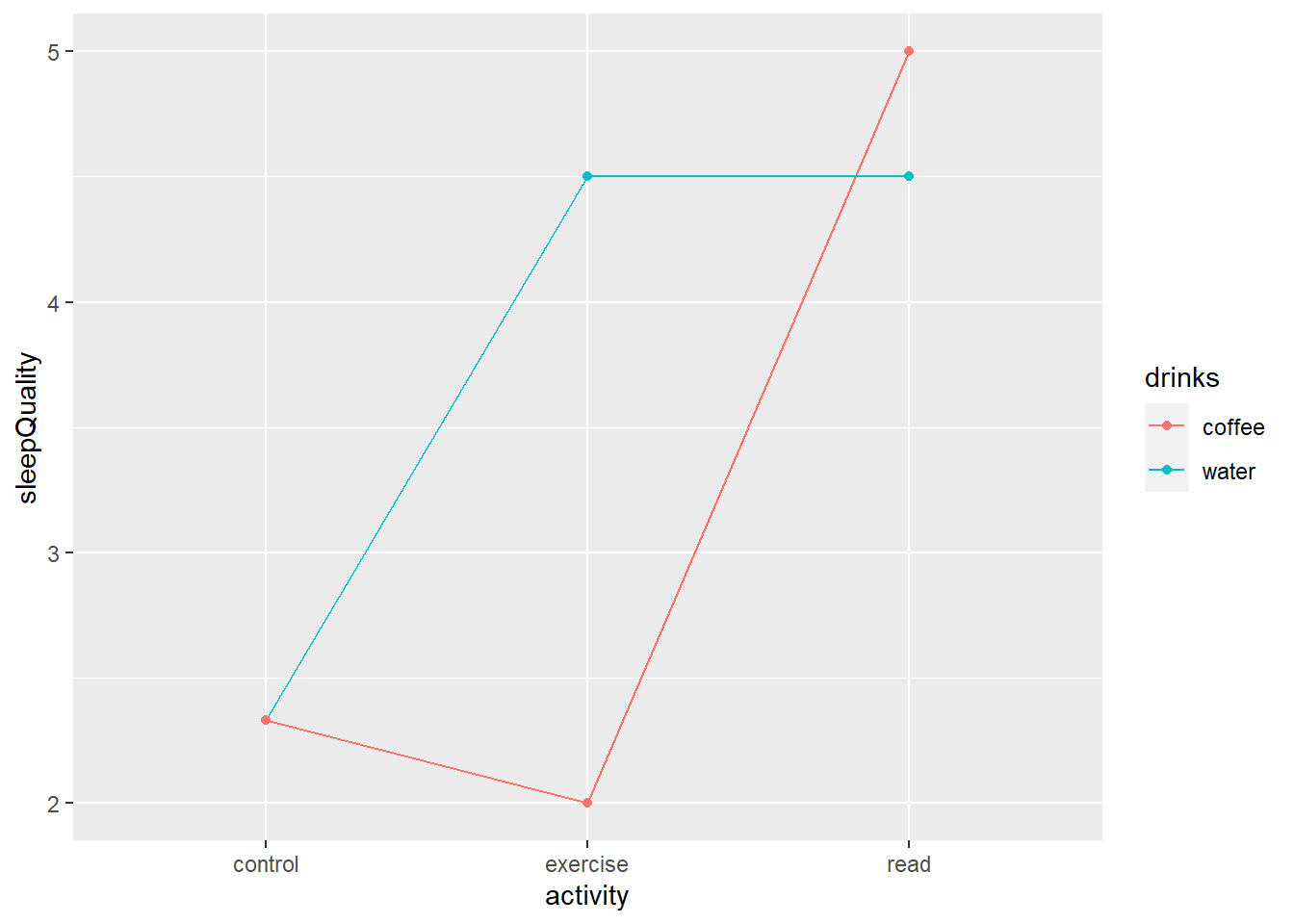
Figuur 27.4: Moderatie geïllustreerd aan de hand van de data over slaapkwaliteit
De figuur laat zien hoe het interactie- of moderatie-effect er precies uitziet. Welke combinatie van categorieën hebben een groot effect op de afhankelijke variabele? De kleuren geven aan wat er is gedronken en op de \(x\)-as staan de categorieën van avondactiviteit. Als de twee lijnen parallel aan elkaar zouden lopen, zou er geen sprake zijn van interactie of moderatie. Het effect van avondactiviteit is dan hetzelfde voor de koffiedrinkers als voor de waterdrinkers. De richting en helling van de lijn zouden dan iets zeggen over het hoofdeffect van avondactiviteit en de afstand tussen de lijnen zou iets zeggen over het verschil tussen de condities koffie en water. Nu er wel sprake is van interactie, kun je de hoofdeffecten niet meer los interpreteren. Je hebt beide factoren tegelijk nodig voor de interpretatie van de effecten.