Hoofdstuk 28 Covariantie-analyse
- statistische controle
- covariaten
- Onderzoekspractium experimenteel onderzoek (PB0422)
28.1 Inleiding
In dit hoofdstuk wordt het begrip statistische controle besproken, een extra middel naast experimentele controle om de ruis in de afhankelijke variabele te verminderen. In het hoofdstuk Experimentele designs is besproken hoe je daarmee ruis in observaties kunt verminderen. Onderzoekers identificeren soms in ANOVA-designs naast de experimentele manipulaties ook vaak belangrijke andere onafhankelijke variabelen die eventuele variatie in de metingen kan helpen verklaren. Deze in het experimentele design opgenomen onafhankelijke variabelen verminderen dan hopelijk de residuele meetfout (onverklaarde variantie), waardoor het effect van de experimentele manipulatie duidelijker zichtbaar wordt: een uitvergroting van het gewenste signaal door het verlagen van verstorende ruis.
In de eerdere hoofdstukken (Variantieanalyse en Factoriele anova) was sprake van ruisvermindering door controlevariabelen toe te voegen aan het experimentele design: deze variabelen werden gemanipuleerd. Deze vorm van ruis verminderen wordt daarom ook wel experimentele controle genoemd.
Het idee van een controlevariabele of ‘controleren voor’ betekent dat het experimentele effect wordt gecorrigeerd voor het effect van een (controle-)variabele. Zo hoopt men te kunnen zien wat het effect van het experiment zou zijn als de controlevariabele er niet was geweest. Het is ook mogelijk om variabelen als deel van het design constant te houden, meestal om het effect van een variabele in een design beter te begrijpen. Zo kan een experimenteel effect onderzocht worden alsof de controlevariabele constant is, meestal door de controlevariabele te vervangen door zijn gemiddelde.
In dit hoofdstuk bespreken we echter een andere manier om ruis (residuele variantie of meetfout) onder controle te houden binnen een experiment. Anders dan in een experimenteel design met goed gekozen manipulaties of groepen om experimentele controle in te bouwen, is het ook mogelijk om variabelen die zich niet (redelijkerwijs) laten manipuleren in de dataverzameling op te nemen. Wanneer variabelen opgenomen worden die niet deel zijn van het experimentele design, maar het doel hebben om residuele variantie in de afhankelijke variabele (onverklaarde variantie) te verklaren, dan spreekt men van statistische controle. De onverklaarde variantie wordt dan niet gecontroleerd via het design, maar via extra rekenwerk in statistische analyses. Variabelen die bij een ANOVA worden gemeten om dienst te doen als statistische controle worden covariaten genoemd. Een ANOVA die één of meer covariaten in de analyse meeneemt wordt een covariantieanalyse genoemd, afgekort met ANCOVA.
28.1.1 De logica achter covariaten
De term ‘covariaat’ heeft verschillende statistische betekenissen. Feitelijk is het een variabele die ‘mee-varieert’ met een andere onafhankelijke (predictor-)variabele bij het voorspellen of verklaren van een afhankelijke variabele. Maar soms wordt er simpelweg een predictorvariabele (onafhankelijke variabele) mee bedoeld die gemeten is op intervalmeetniveau of hoger, in tegenstelling tot een predictor gemeten op nominaal (of soms ook ordinaal) meetnivau, die dan een factor worden genoemd.
Covariaten zijn belangrijke statistische hulpmiddelen wanneer het niet mogelijk is om voor een variabele te controleren op experimentele wijze. Een groot probleem in de communicatie tussen verschillende wetenschappelijke velden is echter dat er veel variatie is in hoe men covariaten definieert. Er zijn wetenschappelijke teksten waar iedere storende variabele een covariaat wordt genoemd. In andere teksten wordt een uiterst strikt onderscheid gemaakt tussen ‘echte’ covariaten, die enkel een relatie met de afhankelijke variabelen mogen hebben, en de meer algemene term voor een storende variabele: confounder.
In deze tekst volgen we de gangbare statistische en theoretische definitie van een covariaat: een covariaat is in een model een predictorvariabele die enkel variantie deelt met de afhankelijke variabele, en niet met de overige predictoren in het model. Andere complexe relaties tussen predictoren, die wiskundig ook covariantierelaties beschrijven, zullen specifiek behandeld worden in andere hoofdstukken (bijvoorbeeld over mediatie). Gelukkig zullen deze verschillende soorten covariaten als statistische controlevariabelen in een ANCOVA dezelfde resultaten opleveren. Iedere predictor in een lineair model gemeten op intervalmeetniveau of hoger heeft in het model de statistisch-wiskundige rol van covariaat, en functioneert uiteindelijk hetzelfde. Het kan wel belangrijk zijn om bij het interpreteren van de resultaten goed in het achterhoofd te houden wat de veronderstelde theoretische relatie van de covariaat was met de overige variabelen in het model. Eventuele inferenties op basis van de covariaat kunnen dan in de juiste context geplaatst worden.
28.1.1.1 Voorbeeld: roken, leeftijd en overlijdensrisico
Een voorbeeld waarbij het zinvol kan zijn om een covariaat op te nemen is als er onderzoek wordt gedaan naar het verband tussen roken (‘ja’ of ‘nee’) en overlijdensrisico (afhankelijke variabele). De onderzoeker weet en heeft in onderzoek bevestigd gezien dat leeftijd ook invloed heeft op het overlijdensrisico. Om te voorkomen dat het verband tussen roken en overlijdensrisico vertroebeld wordt door variatie in leeftijd, kan het opnemen van leeftijd als covariaat zinvol zijn. Door leeftijd in het model op te nemen kan eerst berekend worden hoeveel variantie in overlijdensrisico verklaard wordt door leeftijd. Vervolgens kan worden gekeken hoeveel variantie de variabele roken dan nog uniek verklaart in de afhankelijke variabele overlijdensrisico. Het beeld van het verband tussen roken en overlijdensrisico wordt dus duidelijker door het opnemen van leeftijd als covariaat.
28.1.1.2 Covariaten filteren variantie van storende variabelen
Deze statistische controle met een covariaat is dus zinvol als verwacht wordt dat de covariaat een verband heeft met de afhankelijke variabele (Y). Doordat de covariaat een verband heeft met de afhankelijke variabele, verklaart deze een deel van de variantie van de afhankelijke variabele. Het idee daarachter is dat dit deel van de variantie zogenoemde storende variantie, of ruis is die door het experiment niet verklaard kan worden. En dat gegeven kan worden gebruikt bij het toetsen van een experiment. Het is zinvol om dit te illustreren met sterk vereenvoudigde, conceptuele formules, zodat duidelijker wordt hoe covariaten variantie van storende variabelen kunnen ‘filteren’, dus hoe statistische controle werkt.
De variantie van de afhankelijke variabele (Y) wordt de totale variantie genoemd. De totale variantie beschrijft eigenlijk een model waarbij we enkel weten dat Y varieert, maar waar nog geen onderscheid gemaakt wordt in ‘oorzaken’ van die variantie. In een experiment kunnen condities of manipulaties als onafhankelijke variabelen dienen, en zo de totale variantie helpen opknippen in ‘verklaarde’ delen. Hoe zinvol dit opknippen is betreft eigenlijk de vraag of de experimentele groepen voldoende van elkaar te onderscheiden zijn, en daarom als mogelijke oorzaak van spreiding op Y kunnen worden aangewezen. Zoals eerder beschreven in het hoofdstuk Variantieanalyse wordt de \(F\)-toets in een variantieanalyse gebruikt om te toetsen of een experimentele factor significant variantie van Y verklaart. De definitie van een \(F\)-toets beschrijven we nu in termen die straks helpen te begrijpen wat het toevoegen van covariaten doet:
\[\begin{equation} F=\frac{\text{variantie verklaard door experiment}}{\text{(totale variantie) - (variantie verklaard door experiment)}} \tag{28.1} \end{equation}\]
Dit kan vereenvoudigd worden beschreven als:
\[\begin{equation} F = \frac{\text{tussen-groepenvariantie}}{\text{totale variantie - tussen-groepenvariantie}} \tag{28.2} \end{equation}\]
Het deel onder de deelstreep wordt dikwijls binnen-groepen-variantie genoemd, en kan als ruis worden gezien. Zoals in hoofdstuk Variantieanalyse besproken, drukt de \(F\)-waarde een signaal-ruis-verhouding uit. Hoe groter \(F\) hoe meer verschil er is tussen experimentele groepen in verhouding tot de verschillen tussen individuen binnen die groepen, en dus hoe groter het effect van de manipulatie. Om tot een statistische uitspraak te komen of de \(F\)-waarde hoog of laag is, wordt een bijbehorende \(p\)-waarde berekend. Hoe groter \(F\), des te kleiner wordt \(p\) en dus hoe hoger de kans dat het significant is. Het gevonden verschil tussen de condities wijkt dan immers steeds meer af van wat onder de nulhypothese verwacht mag worden, en het wordt daarmee ook onwaarschijnlijker dat dit door toeval wordt veroorzaakt.
De formule leert ons dat er twee manieren zijn om de \(F\)-waarde te vergroten: (1) boven de deelstreep: de \(F\) kan groter worden door meer tussen-groepen-variantie, dus grotere verschillen tussen groepen, of (2) onder de deelstreep: door de totale (te verklaren) variantie van de afhankelijke variabele te verkleinen. Covariaten zijn een manier om de te verklaren variantie te verkleinen door die verder op te knippen. Aangezien de covariaat een stukje van de variantie van de afhankelijke variabele verklaart, blijft er minder ‘te verklaren’ variantie van Y over. Een formule voor de \(F\)-waarde wanneer een covariaat in het model wordt opgenomen (\(F_c\)) ziet er globaal als volgt uit:
\[\begin{equation} F_c=\frac{\text{variantie verklaard door experiment}}{\text{(totale variantie) - (variantie verklaard door covariaat) - (variantie verklaard door experiment)}} \tag{28.3} \end{equation}\]
Kort samengevat: door covariaten op te nemen is er minder (onverklaarde) binnen-groepenvariantie. Alle variantie in Y die niet aan het experiment kan worden toegeschreven wordt verminderd door de covariaat. Het stukje ‘rest’ dat overblijft in de totale variantie van Y wordt bij het opnemen van een covariaat dus kleiner, wat betekent dat er minder onverklaarde variantie en dus minder ruis in het model is. \(F_c\) is in principe dus altijd groter dan \(F\) en daardoor zal het resultaat bij \(F_c\) een kleinere \(p\)-waarde hebben.
In de figuur hieronder wordt dit idee visueel toegelicht, zie Figuur 28.1. De figuur bestaat uit drie deelfiguren. De eerste deelfiguur (links) toont de situatie zonder covariaat. Het experimentele effect wordt berekend door de overlap van de variantie van de onafhankelijke variabele met de variantie van Y te delen door de variantie in Y die niet overlapt met de afhankelijke variabele. Bij de tweede deelfiguur (in het midden) is er een covariaat toegevoegd die nog een stukje van de variantie van de afhankelijke variabele verklaart. De laatste deelfiguur illustreert hoe de covariaat kan dienen als signaalversterker. De verklaarde variantie van de covariaat is hier uit de cirkel geknipt (figuur rechts). Nu wordt het experimentele effect berekend door de overlap van de varianties van de onafhankelijke variabele en Y te delen door de overgebleven variantie van Y die niet overlapt met de afhankelijke variabele. Doordat er minder onverklaarde variantie van Y is ontstaat er relatief meer verklaarde variantie van de onafhankelijke variabele.
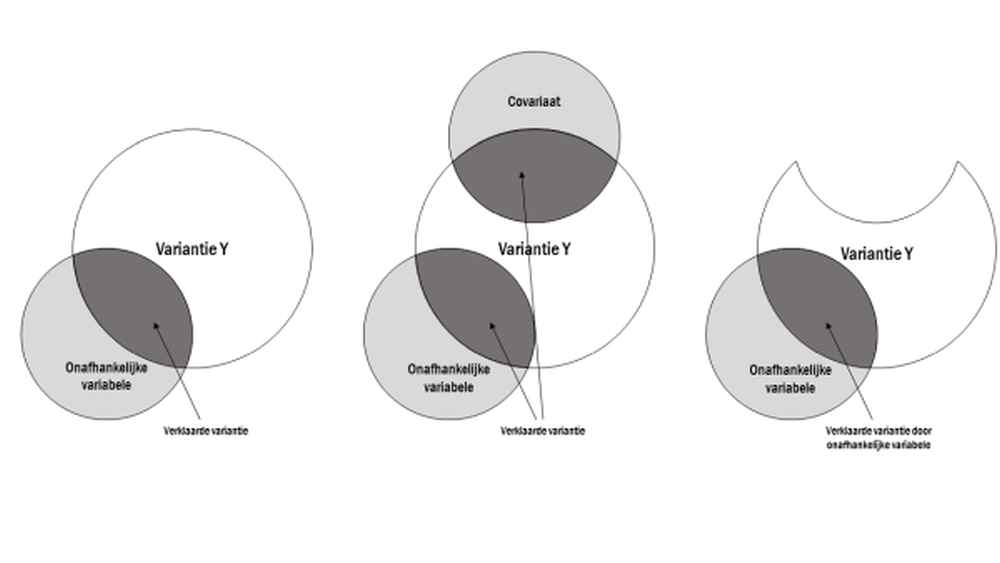
Figuur 28.1: Het Venn diagram illustreert het effect van een covariaat.
Samenvattend kunnen we stellen dat er twee manieren zijn om ruis onder controle te houden. De eerste manier is een experimentele, waarbij correcte randomisatie ervoor zorgt dat de ruis zo klein mogelijk is. De tweede manier is een statistische, waarbij een covariaat wordt toegevoegd om ruis weg te nemen. De experimentele aanpak is te verkiezen, maar is in de praktijk niet altijd mogelijk of niet helemaal optimaal uit te voeren (bijvoorbeeld bij quasi-experimenten). Het gebruik van covariaten kan dan een nuttige aanvulling zijn.
28.2 Hoe werkt statistisch controleren?
Een ANOVA is een lineair model, wat eigenlijk betekent dat het een lineaire regressie ‘in vermomming’ is. Deze kennis is van belang om te begrijpen hoe een covariaat in een model kan controleren voor de effecten van de andere factoren. In Figuren 28.1 en 28.2 wordt getoond hoe er een ‘hap’ uit de variantie van Y wordt genomen. Deze conceptuele visualisatie ligt dichtbij de wiskundige wijze waarop een covariaat in een model onverklaarde variantie verklaart.
Een lineair model met alleen maar covariaten en predictoren is een (meervoudige) lineaire regressie. In een regressiemodel wordt van alle predictoren de unieke verklaarde variantie berekend. Dit wordt gedaan door het effect van een predictor te bepalen wanneer alle overige predictoren en covariaten de waarde ‘nul’ krijgen. Om dit iets duidelijker te maken, worden hieronder enkele vereenvoudigde regressievergelijkingen weergegeven, met een predictor (X), en een covariaat (C) die een afhankelijke variabele (Y) voorspellen.
\[\begin{equation} \hat{Y} = b_0 + b_{1}X + b_{2}C \tag{28.4} \end{equation}\]
Stel dat \(X\) hier een variabele is op nominaal meetniveau, met twee niveaus, bijvoorbeeld controle = 0, en experimenteel = 1. Het gemiddelde, of beter gezegd de verwachte waarde, van \(Y\) voor de controlegroep (dus wanneer \(X = 0\)) is:
\[\begin{equation} \begin{split} \hat{Y} & = b_0 + b_{1}0 + b_{2}C \\ & = b_0 + 0 + b_{2}C \\ & = b_0 + b_{2}C \end{split} \tag{28.5} \end{equation}\]
Er is dus niet echt één gemiddelde waarde van Y voor de controlegroep, omdat het gemiddelde ook nog afhankelijk is van de waarde van de covariaat (er zijn dus meerdere gemiddelden). Om het ‘unieke’ effect van de controleconditie te berekenen, kijken we wat het gemiddelde effect van de controle is, wanneer de covariaat ‘uitstaat’, dus ‘nul’ is in het model:
\[\begin{equation} \begin{split} \hat{Y} & = b_0 + b_{1}0 + b_{2}0 \\ & = b_0 + 0 + 0 \\ & = b_0 \end{split} \tag{28.6} \end{equation}\]
Een intercept heeft geen variabele waarde die op nul gezet kan worden, dus het intercept staat altijd ‘aan’ in het model. Het ‘unieke effect’ van de experimentele groep is dus de waarde van het intercept, plus de ‘meerwaarde’ van de experimentele groep, wanneer de covariaat ‘uit’ wordt gezet, dus waarde nul heeft:
\[\begin{equation} \begin{split} \hat{Y} & = b_0 + b_{1}1 + b_{2}0 \\ & = b_0 + b_{1}1 \end{split} \tag{28.7} \end{equation}\]
Nul is echter niet altijd een realistische waarde van een variabele. Bijvoorbeeld: een IQ van nul is niet mogelijk. En soms betekent de waarde nul niet dat er niets is, maar staat het bijvoorbeeld voor het gemiddelde van een gecentreerde schaal. Gelukkig heeft de betekenis van de waarde nul voor een covariaat vaak geen noemenswaardige gevolgen, zolang er tenminste sprake is van een eenvoudig model waar effecten van covariaten simpelweg worden opgeteld, of waarin slechts één covariaat is opgenomen. Centreren van de covariaat, waardoor zijn gemiddelde nul wordt, kan ook helpen bij de interpretatie.
28.3 Aannames bij covariantieanalyse
Voor een lineair model met covariaten gelden dezelfde aannames zoals besproken in het hoofdstuk Variantieanalyse. Bovenop deze aannames maakt men de volgende aannames:
- Er moet een relatie zijn tussen covariaat en afhankelijke variabele.
- Het effect van de covariaat en de manipulatie zijn onafhankelijk.
- De hellingshoeken van de regressielijnen (‘slopes’) van de covariaat en de afhankelijke variabele zijn in alle experimentele condities gelijk aan elkaar. Dit wordt ‘homogeneniteit van regressie-hellingshoeken’ genoemd (Engels: homogeneity of regression slopes).
Deze aannames worden hieronder besproken.
28.3.1 Er moet een relatie zijn tussen covariaat en afhankelijke variabele
Hoewel het tamelijk triviaal klinkt, wordt vaak vergeten dat enkel sprake is van een covariaat als deze variantie deelt met de afhankelijke variabele. In Figuur 28.1 was te zien waarom: het hele doel van de covariaat is om onverklaarde variantie te verkleinen. De covariaat maakt zo het relatieve aandeel van verklaarde variantie groter en werkt dus als signaalversterker. Zonder gedeelde variantie met de afhankelijke variabele kan de covariaat geen signaal versterken, maar door correlatie met overige predictoren kan die wel de power verlagen. In de volgende paragraaf leggen we dit uit.
28.3.2 Onafhankelijkheid van covariaat en manipulatie
In Figuur 28.1 werd een voorbeeld gegeven van hoe covariaten als een soort signaalversterker kunnen werken door de hoeveelheid onverklaarde variantie te verkleinen. De figuur illustreert gelijk een aantal belangrijke randvoorwaarden, met name het effect van een pure onafhankelijkheid tussen de manipulatie en de covariaat.
In de beschrijving van de logica achter covariaten werd besproken dat covariaten gebruikt kunnen worden om de onverklaarde variantie, de binnen-groepenvariantie, te verminderen, mits de covariaat een deel van deze binnen-groepenvariantie verklaart. In Figuur 28.2 wordt een voorbeeld gegeven van wat er gebeurt zodra de covariaat en manipulatie niet onafhankelijk van elkaar zijn. Links is in het overlappende gebied de verklaarde variantie van de manipuleerde variabelen te zien. In de middelste deelfiguur wordt een covariaat toegevoegd die variantie deelt met de afhankelijke variabele, maar ook met de gemanipuleerde variabele. De gemanipuleerde variabele verklaart nu minder van Y dan zonder covariaat, omdat de covariaat niet alleen ruis ‘weghapt’ maar ook verklaarde variantie. De interpretatie van het effect van de gemanipuleerde variable op Y wordt hierdoor onduidelijk.
In de rechterfiguur wordt zichtbaar wat het effect is van het controleren voor deze covariaat. De overlap tussen de covariaat en de afhankelijke variabele wordt uit de totale variantie van Y geknipt. Maar doordat een deel van die gedeelde variantie overlapte met de gedeelde variantie tussen de gemanipuleerde variable en afhankelijke variabele, wordt ook een stukje van het effect van de manipulatie afgeknipt. Het model heeft minder onverklaarde variantie, maar onbedoeld nu ook minder verklaarde variantie. Hoe groter de overlap tussen de gemanipuleerde variable en de covariaat des te minder ‘uniek’ effect overblijft van de manipulatie.
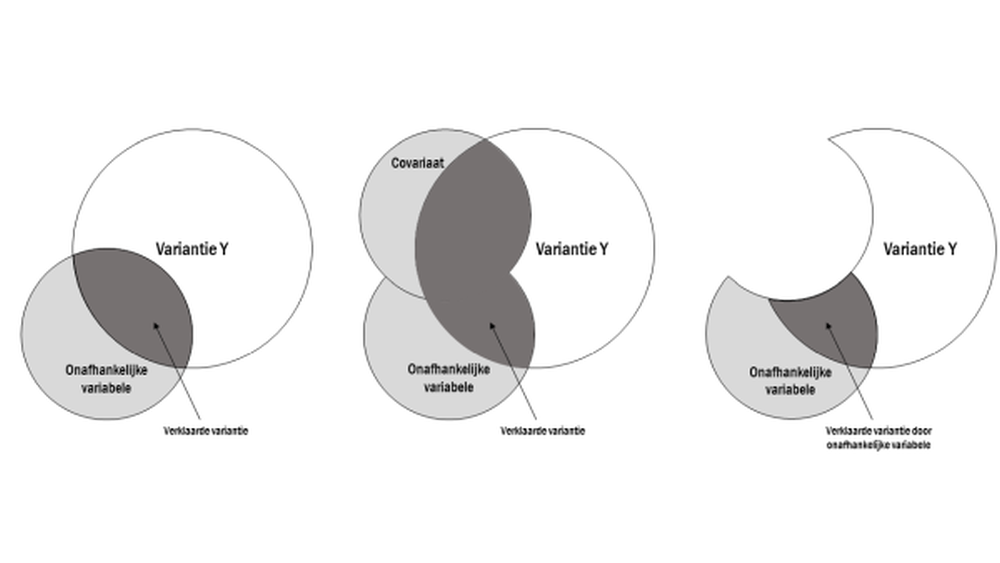
Figuur 28.2: Het Venn diagram illustreert het effect van een covariaat wanneer deze niet onafhankelijk is van de onafhankelijke variabele.
Perfecte onafhankelijkheid, dus een covariantie van nul tussen covariaat en predictor, is in de praktijk utopisch. Zelfs als deze samenhang in de populatie werkelijk nul is zal in een steekproef toch vaak een kleine samenhang gevonden worden. Inferentie vanuit steekproefdata, zoals een significantietest van de samenhang tussen manipulatie en covariaat is een acceptabele manier om te bepalen of de relatie als onafhankelijk mag worden verondersteld (niet te verwarren met het verwerpen van de nulhypothese). Het belangrijkste is echter dat de onafhankelijkheid theoretisch te verdedigen is. Op basis van eerder onderzoek zou bijvoorbeeld duidelijk kunnen zijn dat leeftijd niet samenhangt met het gebruik van bepaalde medicijnen om slaapklachten te verminderen. Leeftijd zou dan als covariaat kunen worden opgenomen in een experiment waarbij deze medicijnen worden getest.
Over de ernst van een schending van de aanname van onafhankelijkheid zijn de meningen scherp verdeeld. Sommigen stellen dat enkel bij complete onafhankelijkheid een covariantieanalyse geoorloofd is. Wanneer de assumptie van onafhankelijkheid geschonden is, mag men volgens deze strikte statistici de uitkomsten van een ANCOVA slechts met zeer grote voorzichtigheid interpreteren. De auteurs van dit hoofdstuk nemen een meer pragmatische positie in, en erkennen dat perfecte onafhankelijkheid niet heel realistisch is. Toch benadrukken ook wij dat de effecten van het schenden van de aanname van onafhankelijkheid niet voldoende serieus genomen worden in veel gepubliceerd onderzoek. Wanneer de covariaat en manipulatie variantie delen kun je eigenlijk niet meer controleren voor het effect van de covariaat.
28.3.2.1 Een voorbeeld van afhankelijkheid van covariaat en predictor
Stel dat een onderzoeker de relatie tussen depressie en een slaapproblemen wil weten. Als de onderzoeker voor ruis wil corrigeren door angst als variabele op te nemen in het model, dan ontstaat er eigenlijk bij voorbaat al een probleem. Angst en depressie hangen namelijk duidelijk samen. Hoe hoger de depressiescore, des te hoger zal de angstscore zijn. Dit leidt dan tot de situatie zoals weergegeven in Figuur 28.2. Het is niet mogelijk om een goed beeld te krijgen van het ‘pure’ effect van depressie of angst. Het is hoogstens mogelijk om te berekenen wat het ‘unieke’ effect van de variabelen is, als de overlappende variantie genegeerd wordt. Dit kan een waardevolle vraag zijn (zie bijvoorbeeld hoofdstuk multipele-regressie), maar het is niet een situatie waar statistische controle (zinvol) plaatsvindt.
Het is niet verboden om een ANCOVA uit te voeren wanneer covariaat en onafhankelijke variabele niet onafhankelijk zijn, maar in de regel is het beter om het niet te doen. Als een covariaat toch in een model wordt opgenomen, dan moet er bij de interpretatie specifiek aandacht besteed worden aan de mate van overlap, en de mogelijke impact daarvan op de conclusies.
Het toetsen van de onafhankelijkheid tussen covariaat en onafhankelijke variabele wordt meestal gedaan door een statistische toets uit te voeren met de onafhankelijke variabele als predictor, en de covariaat als afhankelijke variabele. Welke toets dat zal moeten zijn, hangt af van de meetniveaus van de variabelen. De hoop bij deze toets is dat de \(p\)-waarde niet significant is (en de nulhypothese dus niet verworpen wordt) en de effectgrootte klein is. Er zijn geen harde regels over wanneer er wel of geen verband mag worden verondersteld. Zo’n statistische toetsing van onafhankelijkheid kan helpen bij het besluiten om een covariaat weg te laten (dus toch maar niet als covariaat te zien). Maar ze zou niet gebruikt moeten worden om te besluiten of een covariaat toegevoegd zou moeten worden. De keuze om een covariaat aan het model toe te voegen moet namelijk geen statistische keuze zijn, maar een theoretische.
28.3.3 Homogeneniteit van regressie-hellingshoeken
Bij een covariaat wordt niet alleen aangenomen dat deze geen variantie deelt met de onafhankelijke variabele. Er wordt ook vanuit gegaan dat de covariaat voor alle waarden van de onafhankelijke variabele dezelfde relatie heeft met de afhankelijke variabele. Dit lijkt op het eerste gezicht weer te gaan over de onafhankelijkheid van covariaat en onafhankelijke variabele. Dat is deels waar, maar de assumptie van homogeniteit van regressie-hellingshoeken (Engels: homogeneity of regression slopes) is iets specifieker. Het is eigenlijk een manier om te zeggen ‘De samenhang tussen covariaat en afhankelijke variabele moet steeds hetzelfde zijn, ongeacht de waarde die de onafhankelijke variabele aanneemt’.
In sectie 28.4 wordt met behulp van een regressievergelijking uitgelegd hoe waarden van de afhankelijke variabele, bijvoorbeeld groepsgemiddelden, afhangen van de covariaat. Dus, hoe je cijfermatig ‘controleert’ voor een variabele. Wanneer het effect tussen covariaat en afhankelijke variabele verschilt per waarde van de onafhankelijke variabele, dus wanneer er een interactie-effect is tussen covariaat en onafhankelijke variabele op de afhankelijke variabele, dan klopt het basismodel met alleen maar hoofdeffecten inclusief covariaat niet meer. Eenvoudiger gezegd: de covariaat ‘controleert’ niet meer voor iets. De covariaat is niet meer een stille controlefactor op de achtergrond, maar speelt nu een hoofdrol in het verklaren van de afhankelijke variabele. De interactie suggereert dat groepsverschillen in de afhankelijke variabele variëren als een functie van de covariaat. Of dat het effect van de covariaat op de afhankelijke variabele afhangt van de experimentele condities.
Helaas is er niet echt een oplossing voor een situatie waarin de covariaat interacteert met de manipulatie. Het is in ieder geval sterk om de interactieterm in het model te laten, dus de interactieterm wel te schatten. Het interpreteren van de interactie kan interessant zijn, en kan eventueel in de discussiesectie van een verslag meegewogen worden in het verklaren van de resultaten. Het is dan belangrijk om de resultaten met voorzichtigheid te verklaren; door de interactie tussen covariaat en manipulatie in het model is het niet meer mogelijk om de verschillen tussen groepen te bespreken zonder ook de covariaat in het verhaal te betrekken.
In Figuren 28.3 en 28.4 is een relatie tussen een covariaat (C) en een afhankelijke variabele (Y) weergegeven voor drie condities (groepen). Als de covariaat geen interactie heeft met de onafhankelijke variabele en dus de hellingshoeken van de regressielijn ‘homogeen’ zijn, dan zouden de lijnen hetzelfde moeten lopen, zoals in Figuur 28.3 afgebeeld. Ze zouden dus dezelfde steilheid moeten hebben. In Figuur 28.3 is bijvoorbeeld te zien hoe de drie vergeleken groepen ieder een ander gemiddelde hebben, maar dat het gemiddelde van Y ook beïnvloed wordt door de covariaat.
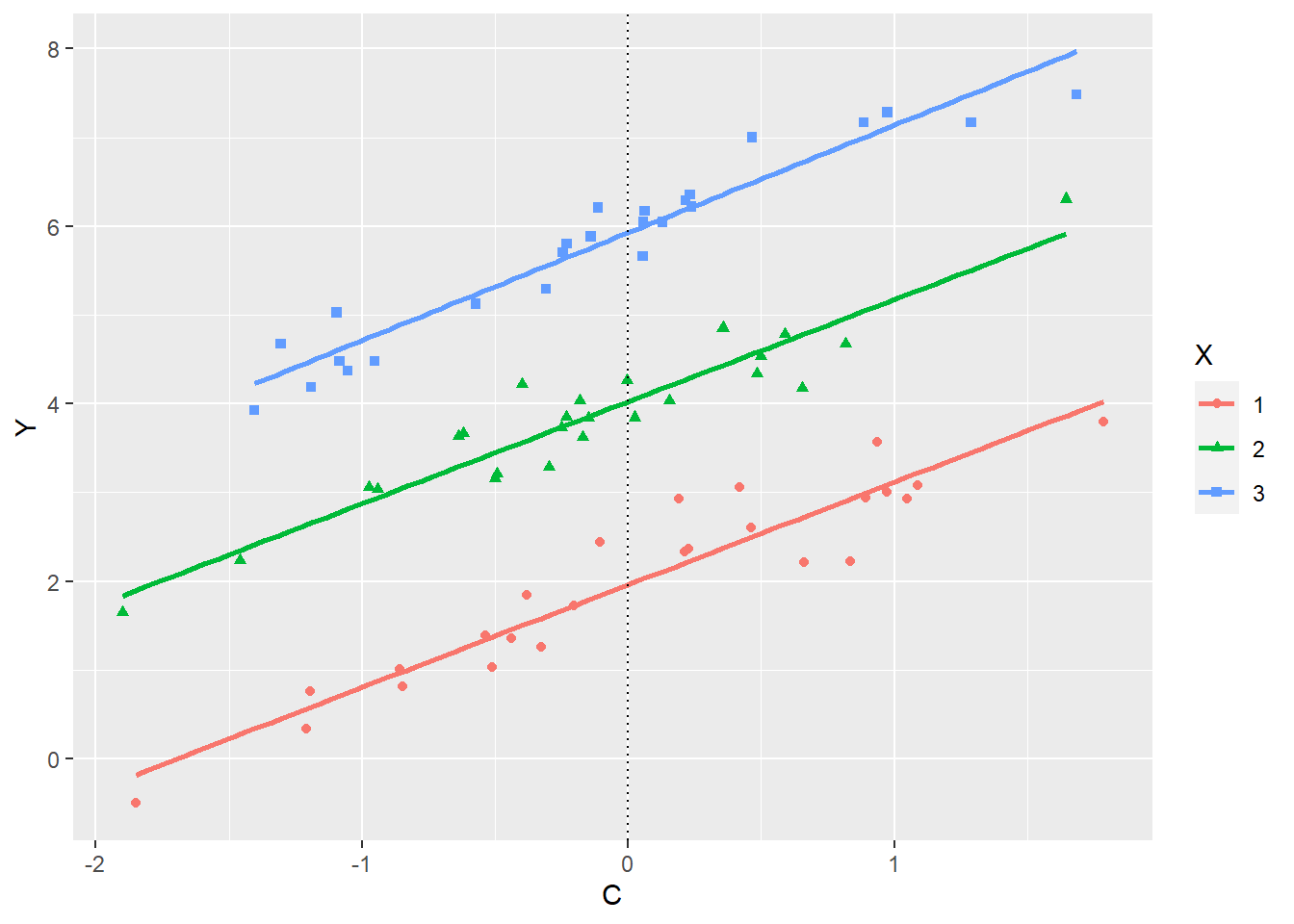
Figuur 28.3: Voorbeeld van een effect van een covariaat C op afhankelijke variabele Y, waarbij de hellingshoek (het effect) van covariaat C onafhankelijk is van X, waardoor de hellingshoeken homogeen zijn
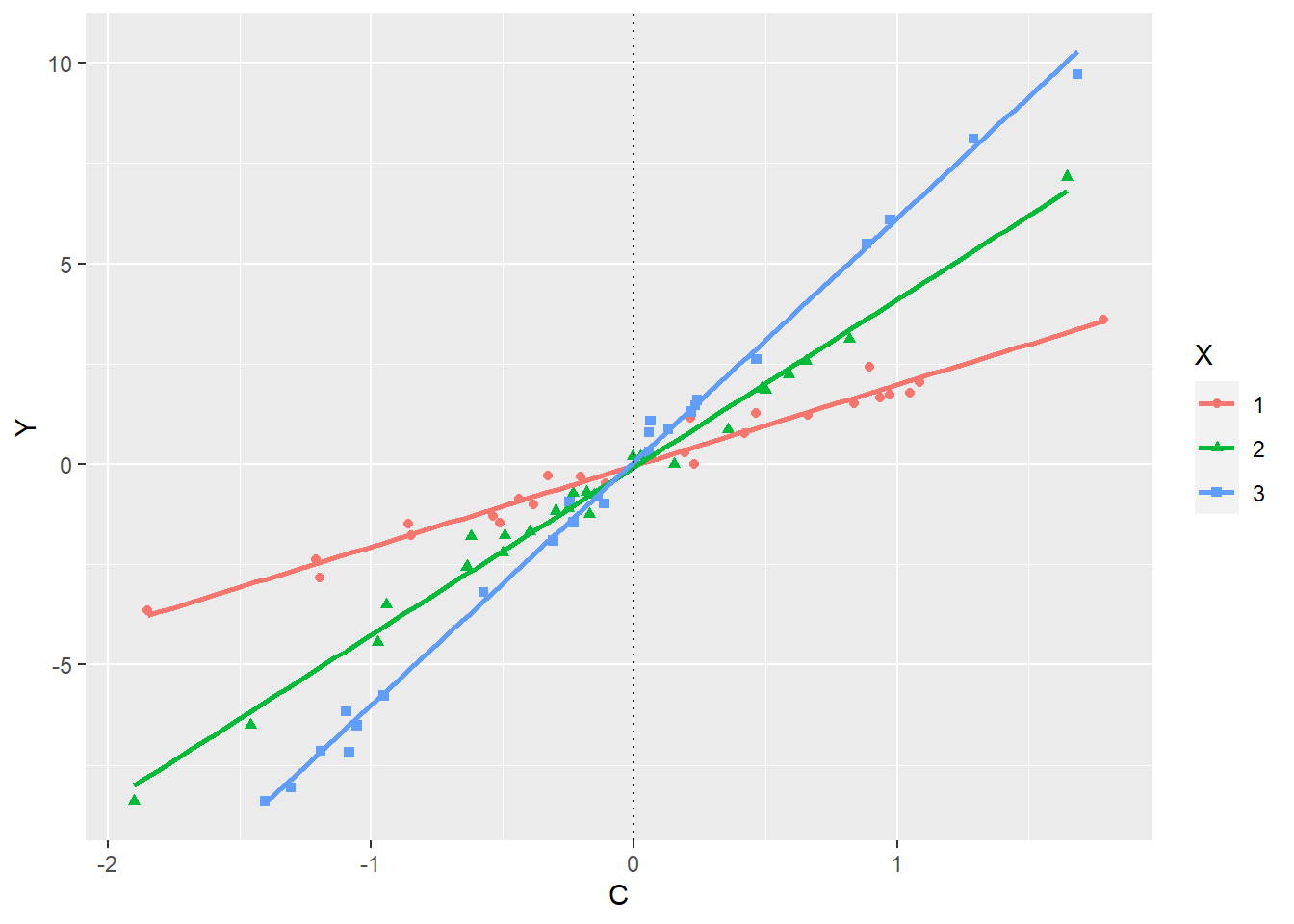
Figuur 28.4: Voorbeeld van een effect van een covariaat C op afhankelijke variabele Y, waarbij de hellingshoek (het effect) van X afhankelijk is, dus interacteert met X
De verticale stippellijn in de figuur geeft aan hoe het model met covariaataanpassing omgaat: als de waarde van de covariaat op nul gezet wordt (zie sectie 28.2 ) dan valt af te lezen wat de voor de covariaat aangepaste gemiddelden zouden zijn. Het maakt niet echt uit waar precies de stippellijn geplaatst wordt. Waar de lijn ook is, de relatieve afstand tussen de drie groepen blijft hetzelfde. De geschatte gemiddelden veranderen wellicht, maar bij het bepalen of er een effect is van X op Y kan er probleemloos een doorsnede gemaakt worden op een willekeurige waarde van C om tot dezelfde conclusie te komen over het effect.
Anders is dit in Figuur 28.4. Als het effect van X beoordeeld wordt wanneer de covariaat wordt ‘uitgezet’, dus waarde nul krijgt, dan zou een onderzoeker tot de conclusie komen dat de groepen helemaal niet verschillen van elkaar, of dat alle verschillen toe te schrijven zouden zijn aan de covariaat in plaats van de manipulatie.
Maar deze interpretatie zou onjuist zijn. De covariaat heeft niet hetzelfde effect voor iedere groep; afhankelijk van de manipulatie kan de covariaat een sterk of zwak effect op de afhankelijke variabele hebben. Als er op een willekeurige waarde van de covariaat een dwarsdoorsnede zou worden gemaakt, dan zouden er tegenstrijdige conclusies mogelijk zijn: bij een waarde van de covariaat onder nul is het effect van X precies het omgekeerde van het effect wanneer de covariaat boven de nul is. Het is hier niet mogelijk om over het effect van de manipulatie of de covariaat te spreken zonder de relatie tussen manipulatie en covariaat te benoemen. Een ‘blinde’ aanpassing van het model voor de covariaat vertekent de resultaten.
De meningen zijn erg verdeeld over de consequenties van de schending van de assumptie van homogene regressie-hellingshoeken. Er hoort geen interactie tussen covariaat en onafhankelijke variabele te zijn op de afhankelijke variabele. Maar er zijn gevallen waar dit nu juist wel verwacht wordt. Wanneer een onderzoeker het effect onderzoekt van feedback geven op motivatie dan zal zij tegen de situatie aanlopen dat scholen verschillen in het niveau van de leerlingen. Op een school in een buurt met veel zwakpresterende leerlingen zal feedback eerder als kritiek ervaren worden, terwijl hoogpresterende leerlingen feedback vaak meer verwelkomen. Wanneer de onderzoeker statistisch wil controleren voor prestatieniveaus van de leerlingen, dan kan het zijn dat het effect van feedback op motivatie versterkt wordt (of gedempt) door prestatieniveau. Het is dus niet mogelijk om in het algemeen prestatieniveau uit de onverklaarde variantie te knippen. De interactie moet dan expliciet in het model meegenomen worden. Hiervoor zijn andere analysetechnieken ontwikkeld.
Samenvattend: bij het opnemen van een covariaat in het model is het belangrijk om te toetsen of er een ongeoorloofd interactie-effect is tussen covariaat en onafhankelijke variabele op de afhankelijke variabele. Als dit er wel is (significant en een voldoende grote effectgrootte), dan moet eigenlijk de interactieterm behouden blijven in het model dat gebruikt wordt om de onderzoeksvraag te beantwoorden. Als dit tot lastige interpretaties van de data leidt is het ook te rechtvaardigen om de covariaat niet in het model op te nemen, zeker als ook andere assumpties geschonden worden.
28.4 Voorbeeld: covariaten in het lineaire model
In de context van variantieanalyse, waarin het doel is om gemiddelden tussen groepen mensen te vergelijken, kunnen ook modellen worden gebruikt waarin een of meer continue (numerieke) predictorvariabelen worden opgenomen. In de hoofdstukken over oneway-ANOVA (hoofdstuk Variantieanalyse) en factoriële ANOVA (hoofdstuk Factoriele-anova) hebben we variantieanalyse al besproken als een lineair model met dummy-variabelen. Het is daarom niet moeilijk om te begrijpen dat we om een extra variabele op te nemen, nu alleen nog maar een term hoeven toe te voegen aan een dergelijk model.
De belangrijkste reden om een covariaat in een model op te nemen is in de inleiding uitgelegd en herhalen we nogmaals. Als we verwachten dat een bepaalde variabele (niet zijnde de predictor) samenhangt met de afhankelijke variabele dan nemen we deze variabele op als covariaat in het model, zodat er meer variantie van de afhankelijke variabele kan worden verklaard en de residuele variantie afneemt. De residuele variantie is de variantie van de afhankelijke variabele binnen de experimentele groepen. Het gevolg is dat de power van het effect van de experimentele manipulatie naar verwachting toeneemt. Een effect wordt namelijk eerder zichtbaar, in de zin van statistisch significant, als er minder ruis is.
28.4.1 Voorbeeldanalyse van slaapkwaliteitdata
De conceptuele logica achter statistische controle voor een covariaat door ANCOVA is tamelijk rechtoe-rechtaan. De ANCOVA past de gemiddelden van de afhankelijke variabele in iedere experimentele conditie aan op basis van de waarde van de covariaat. Als een van de condities een bovengemiddelde score had op de covariaat in vergelijking tot andere condities, dan wordt van deze groep de gemiddelde score op de afhankelijke variabele naar beneden bijgesteld. Een conditie met een ondergemiddelde score op de covariaat in vergelijking tot andere groepen zal op de afhankelijke variabele naar boven bijgesteld worden. Hoeveel moet worden bijgesteld hangt af van de omvang van het verschil tussen de gemiddelde covariaatscore van de conditie en het totale gemiddelde van de covariaat. Zo wordt statistisch nagebootst dat de groepen vergeleken worden alsof de covariaat in iedere conditie hetzelfde gemiddelde had.
Als voorbeeld gebruiken we de eerder gebruikte slaapkwaliteitdata.
In het hoofdstuk over Oneway-ANOVA) was de gerapporteerde slaapkwaliteit de afhankelijke variabele met één predictor, genaamd ‘avondactiviteit’. Het experiment bestond uit drie condities die men een week moest volhouden: lezen, sporten, controle. In het hoofdstuk over Factoriele-anova, werd een tweede factor geïntroduceerd, die ‘drank’ werd genoemd. Deze factor bestaat uit twee categorieën (condities): koffie en water. Hiervoor gold dat men ofwel de hele avond een hoeveelheid koffie moest drinken, of enkel water. De twee factoren waren volledig gebalanceerd, wat wil zeggen dat alle combinaties van condities mogelijk waren en dat elke combinatie van condities ongeveer evenveel proefpersonen telde.
Bij dit 2x3-factoriële design meten we ook de leeftijd van de respondenten. We verwachten namelijk dat leeftijd samenhangt met slaapkwaliteit, bijvoorbeeld de slaapkwaliteit neemt af met het verloop van de jaren. We nemen leeftijd dus op in het model als covariaat.
Als voorbeeld bespreken we het model met de variabele avondactiviteit als experimentele manipulatie en leeftijd als covariaat om slaapkwaliteit te verklaren. Voor de variable avondactiviteit gebruiken we de dummy-variabelen ‘exercise’ en ‘read’. De variabele ‘age’ is een numerieke variabele en die kunnen we direct opnemen in het model.
\[\begin{equation} \text{sleepQuality} = b_0 + b_1\mathrm{exercise} + b_2\mathrm{read} + b_3\mathrm{age} + \varepsilon \tag{28.8} \end{equation}\]
Allereerst bekijken we de parameterschattingen. In de volgende tabel worden eerst de parameterschattingen getoond van de analyse zonder covariaat (model1) en daarna met covariaat (model2).
| Estimate | Std. Error | t value | Pr(>|t|) | 2.5 % | 97.5 % | |
|---|---|---|---|---|---|---|
| model1 | ||||||
| (Intercept) | 2.33 | 0.42 | 5.6 | 0.00 | 1.48 | 3.18 |
| exerciseD | 0.92 | 0.59 | 1.6 | 0.13 | -0.29 | 2.12 |
| readD | 2.42 | 0.59 | 4.1 | 0.00 | 1.21 | 3.62 |
| model2 | ||||||
| (Intercept) | 5.18 | 1.12 | 4.6 | 0.00 | 2.91 | 7.46 |
| exerciseD | 0.56 | 0.56 | 1.0 | 0.33 | -0.58 | 1.69 |
| readD | 2.12 | 0.55 | 3.8 | 0.00 | 1.00 | 3.25 |
| age | -0.06 | 0.02 | -2.7 | 0.01 | -0.11 | -0.02 |
28.4.2 Voorbeeld: berekenen van de voor de covariaat aangepaste gemiddelden
De betekenis van de parameterschattingen zijn uitgelegd in het hoofdstuk over oneway-ANOVA (hoofdstuk Variantieanalyse). De schattingen representeren (een functie van) de groepsgemiddelden. Om dat goed te zien, zijn in de volgende tabel (Tabel 28.2) de groepsgemiddelden getoond. Het gemiddelde van de controlegroep is onmiddelijk terug te vinden als het intercept van model \(1\). Tellen we hier de schatting van het ‘exercise’-effect bij op dan is dat het gemiddelde van de conditie ‘exercise’. Hetzelfde valt te zien voor de conditie ‘read’. Maar wat betekenen de parameterschattingen van model \(2\), het model met de covariaat?
| activity | sleep | age |
|---|---|---|
| control | 2.3 | 47 |
| exercise | 3.2 | 41 |
| read | 4.8 | 42 |
| totaal | 3.4 | 44 |
Om dit te begrijpen moeten eerst de voorspellingen door het model worden berekend. Deze voorspellingen worden ook wel de estimated marginal means genoemd. Bij ANCOVA worden deze estimated marginal means voor het eerst belangrijk, omdat het berekenen hiervan de enige manier is om gemiddelden te berekenen die aangepast zijn voor de covariaat. Als we alleen dummy-variabelen hebben is dat gemakkelijk omdat we voor de dummy alleen een \(1\) of een \(0\) kunnen invullen. De bij de dummy behorende variabele telt dan of wel (dummy = \(1\)) of niet mee (dummy = \(0\)). Maar wat moeten we invullen voor een numerieke variabele zoals hier de covariaat leeftijd?
Om dat te verduidelijken beginnen we met de controlegroep, waarbij beide dummies in het model \(0\) zijn. Voor leeftijd vullen we simpelweg de gemiddelde leefijd in van alle deelnemers, zie tabel.
\[\begin{equation} sleepQuality =\\ 5.18 + b_1 \times 0 + b_2 \times 0 + -0.06\times 43.69 = 2.56 \tag{28.9} \end{equation}\]
Vervolgens doen we dit ook voor respectievelijk de groepen ‘exercise’ en ‘read’.
\[\begin{equation} \text{sleepQuality} =\\ 5.18 + 0.56 \times 1 + b_2 \times 0 + -0.06\times 43.69 = 3.12 \tag{28.10} \end{equation}\]
\[\begin{equation} \text{sleepQuality} =\\ 5.18 + b_1 \times 0 +2.12 \times 1 + -0.06\times 43.69 = 4.68 \tag{28.11} \end{equation}\]
Er zijn nu drie aangepaste gemiddelden (adjusted means) berekend: de voorspelde gemiddelde slaapkwaliteit in de drie condities, gegeven dat de personen de gemiddelde leeftijd van de totale groep hadden. In de tabel met de resultaten van model \(2\), kan nu betekenis gegeven worden aan de parameterschattingen: het blijkt dat deze schattingen op dezelfde manier als de schattingen van model \(1\) een functie van de aangepaste groepsgemiddelden representeren. Bijvoorbeeld: de parameterschatting van ‘exercise’ (0.56, zie Tabel 28.1) geeft het verschil in aangepaste gemiddelden weer tussen de controlegroep en de exercise-groep,
\[3.12 - 2.56 = 0.56\]
De betekenis van de andere parameterschattingen kan op analoge wijze worden afgeleid. In bovenstaande formules hebben we de gemiddelde leeftijd ingevuld, maar we hadden ook een willekeurige andere leeftijd kunnen invullen. Dat maakt wel verschil voor de voorspelde slaapkwaliteit, die verschilt namelijk per leeftijd, maar voor de verschillen tussen condities maakt het niet uit. Het is eenvoudig te zien in de formules dat de term die correspondeert met leeftijd eruit valt bij het berekenen van verschillen tussen gemiddelden, omdat deze term constant is. De interpretatie van een parameterschatting is dus het verschil in de voorspelde gemiddelden van slaapkwaliteit tussen de desbetreffende conditie en de controlegroep, gegeven dat de leeftijd constant is.
Tenslotte is er nog de betekenis van het intercept. Dit is de waarde van slaapkwaliteit als alle andere termen in het model \(0\) zijn. In model \(1\) is dit simpelweg de gemiddelde slaapkwaliteit van de controlegroep, omdat de twee dummies daar \(0\) zijn. Voor model \(2\) geldt ook dat alle termen \(0\) moeten zijn om de betekenis van het intercept te duiden. In het model moet dus ook de term van de covariaat \(0\) zijn en die is alleen \(0\) als de leeftijd \(0\) is. Het intercept is dus de voorspelde slaapkwaliteit voor mensen in de controleconditie met leeftijd gelijk aan \(0\), babies dus. Hoewel de waarde \(0\) voor leeftijd in principe mogelijk is en de uitkomst eigenlijk niet eens heel vreemd is, is het meestal beter om variabelen te centreren (rondom hun gemiddelde) zodat de waarde \(0\) voor de gecentreerde variabele correspondeert met het gemiddelde van die variabele (in dit voorbeeld leeftijd) in de steekproef. De betekenis van het intercept is dan de voorspelde slaapkwaliteit van mensen in de controleconditie met een gemiddelde leeftijd.
In Tabel 28.3 staan de resultaten van de analyse met leeftijd gecentreerd. De gecentreerde variabele wordt weergegeven met ’_c’ achter de naam (hier: age_c), waardoor het meteen duidelijk is dat deze variabele is gecentreerd. De parameterschattingen zijn hetzelfde als voorheen, behalve voor het intercept. Het intercept representeert nu de voorspelde slaapkwaliteit van mensen in de controleconditie met een gemiddelde leeftijd. Zie formule (28.9), waarin deze waarde werd uitgerekend.
| Estimate | Std. Error | t value | Pr(>|t|) | 2.5 % | 97.5 % | |
|---|---|---|---|---|---|---|
| (Intercept) | 2.55 | 0.39 | 6.5 | 0.00 | 1.76 | 3.35 |
| exerciseD | 0.56 | 0.56 | 1.0 | 0.33 | -0.58 | 1.69 |
| readD | 2.12 | 0.55 | 3.8 | 0.00 | 1.00 | 3.25 |
| age_c | -0.06 | 0.02 | -2.7 | 0.01 | -0.11 | -0.02 |